September 2019 ~ Ruang Belajar Matematika

Rabu, 25 September 2019

Cara Mengetik Rumus atau Simbol Matematika di Blog

Assalamu'alaikum . .
Sobat Blgger, pada awal post di kolom Tips dan Trik ini saya mencoba berbagi info cara mengetik Rumus atau Simbol Matematika di Blog.
Baik langsung saja kita mulai mempraktekkannya....

Misalkan kita akan mengetik Rumus berikut
$S_{n}=\, \frac{n}{2}[2a+(n-1)b]$
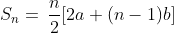
langkah-langkahnya ialah,
Pertama saya anggap sobat telah login di Blogger
1. Buat Entri baru
2. Posisi Cursor di halaman posting, sementara itu silakan sobat login ke https://www.codecogs.com/latex/about.php atau di kolom pencarian ketik "codecogs.com" tanpa tanda petik lalu enter > pilih dan klik Equation Editor

pada jendela Equation Editor klik Screenshot

maka akan muncul jendela pop up seperti berikut

di ruang berwarna kuning itulah tempat mengetik huruf dan simbol matematika dalam bentuk kode HTML dan hasilnya berada di bagian bawahnya, seperti berikut

Untuk rumus di atas ketik kode HTML atau bisa mengambil dari menu di atasnya seperti berikut:

S_{n}=\frac{n}{2}[2a+(n-1)b]

3. Kemudian copy hasilya dan tempel di tempat posting, selesai...
4. Lihat hasilnya dengan klik Pratinju

Selamat mencoba........
Demikian semoga bermanfaat dan terima kasih telah mampir di Blog kami

Pembahasan Soal Deret Aritmetika

15.42 Soal-soal SMP No comments

Salah satu keponaan bertanya cara menyelesaikan soal berikut,
Soal:
Temukan tiga bilangan ganjil berurutan yang jumlahnya sama dengan 45

Penyelesaian:
Soal tersebut jika diselesaikan dengan cara Barisan / Deret sbb:
"tiga bilangan ganjil berurutan yang jumlahnya sama dengan 45", ini termasuk Deret Aritmetika, maka dapat ditentukan
U₁ = a    U₂ = a + 2    U₃ = a + 4 catatan: ditambah 2 karena selisih bilangan
ganjil berurutan sama dengan 2
b = 2 dan   S_n = 45
$S_{n}=\, \frac{n}{2}[2a+(n-1)b]$
$45=\, \frac{3}{2}[2a+(3-1)2]$
45 x 2 = 3(2a + 4)
90 = 6a + 12
90 - 12 = 6a
78 = 6a
a = 13   U₁ = 13
  U₂ = a + 2 = 13 + 2 = 15
  U₃ = a + 4 = 13 + 4 = 17
Jadi bilangan-bilangan ganjil itu adalah 13 , 15 dan 17

Menyelesaikan Persamaan Kuadrat dengan Menfaktorkan

16.41 SMP Kelas IX No comments

Persamaan Kuadrat
$Bentuk \, Umum\, \, \mathbf{ax^{2}+bx+c=0}\, dengan\, a\neq 0\,dan\, a,b,c\in R$
dimana x adalah variabel dan a, b, c disebut koefisien persamaan kuadrat
Contoh: 2x² + 5x – 3 = 0           a = 2 ,   b = 5 ,   c = -3
3x² + 9x = 0                 a = 3 ,   b = 9 ,   c = 0
  x² – 25 = 0                   a = 1 ,   b = 0 ,   c = -25

Nilai x yang memenuhi persamaan ax² + bx + c = 0 , disebut akar-akar atau penyelesaian dari persamaan tersebut.

Menyelesaikan Persamaan Kuadrat dengan Menfaktorkan
Jika $\mathbf{p,q\in R}$ dan  pq = 0, maka p = 0 atau q = 0

Sifat diatas dapat digunakan setelah bentuk ax² + bx + c = 0 difaktorkan terlebih dahulu dengan cara:
1. Faktorisasi dengan hukum Distributif
   $\mathit{ax^{2}+abx=ax(x+b)}$
   $\mathit{px^{2}-pqx=px(x-q)}$
2. Faktorisasi Selisih Dua Kuadrat
   $\mathit{x^{2}-y^{2}=(x+y)(x-y)}$
3. Faktorisasi bentuk ax² + bx + c , dengan a = 1
  ax² + bx + c = (x + p)(x + q)
  c = p × q   catatan : p dan q bilangan bulat
  b = p + q
4. Faktorisasi bentuk ax² + bx + c , dengan $a\neq 1$
  ax² + bx + c = ax² + px + qx + c
=  ax² +(p + q)x + c

p × q = a × c catatan : p dan q bilangan bulat
p + q = b

Contoh:
Tentukan akar-akar persamaan kuadrat  x² – 7x + 12 = 0
Jawab:
x² – 7x + 12 = 0, dimana persamaan kuadrat ini berbentuk  ax² + bx + c , dengan a = 1

cara penyelesaiannya sbb

nilai c = 12 nilai faktor 12 = -4 x (-3)

b = -7 nilai jumlah -7 = -4 + (-3), maka diperoleh penfaktoran

x² – 7x + 12 = 0

(x - 4)(x - 3) = 0

x - 4 = 0 atau x - 3 = 0

x₁ = 4 x₂ = 3

Titik Nol

09.02 Matematika ImTaq No comments

Kembali ke Titik Nol

Assalamu'alaikum wr. wb.
Sungguh Alloh swt. maha penyayang terhadap hambaNya, yang dengan pasti memberi ampunan bagi seorang hamba yang setiap melaksanakan Ibadah Mahdhah (a.l sholat, puasa haji) akan dihapus dosanya, artinya orang tersebut "kembali ke titik nol" bersih dari dosa.

Ditinjau dari sudut Ilmu Matematika, kembali ke titik nol ialah bergerak memutar ke kiri sejauh 360^o (dari titik 0^o kembali ke 0^o lagi)

Sebagai contoh gerakan ibadah sholat
Coba kita perhatikan gerakan sholat yang kita lakukan mulai dari awal (takbir):
Pertama: takbiratul ihram, "berserah diri secara total" pada Alloh swt bernilai 0^o , dan berdiri tegak membentuk sudut 180^o

Kedua: ruku', badan dan kaki membentuk sudut 90^o (siku-siku)

Ketiga: sujud, membentuk sudut 45^o sebanyak dua kali, demikian selanjutnya kembali berdiri untuk rakaat berikutnya.

Total satu rakaat gerakan sholat bergerak 360^o ( 180^o + 90^o + 45^o +45^o ) dan kembali ke titik 0^o "nol". Demikian juga untuk rakaat berikutnya, Subhanalloh....

Waallahua'lam bisshowab.

Pembahasan Soal Trigonometri

05.41 Soal-soal SMA No comments

Soal:
Jika   $\sec \alpha -\tan \alpha = x$ untuk $0^{o}< \alpha < 90^{o}$ , tentukanlah $\left ( \tan \alpha +\sec \alpha \right )$

Penyelesaian:
$\sec \alpha -\tan \alpha = x$
$(\sec \alpha - \tan \alpha )^{2} = x^{2}$
Uraian 1: $(\sec \alpha - \tan \alpha )^{2} = x^{2}$
   $\sec ^{2}\alpha -2.\sec \alpha.\tan \alpha + \tan ^{2}\alpha =x^{2}$
$\tan \alpha +1-2.\sec \alpha .\tan \alpha +\tan ^{2}\alpha =x^{2}$
$2.\tan ^{2}\alpha -2.\sec \alpha .\tan \alpha =x^{2}-1$
$2.\tan \alpha (\tan \alpha -\sec \alpha )=x^{2}-1$
$-2.\tan \alpha (\sec \alpha -\tan \alpha )=x^{2}-1$
   $-2.\tan \alpha .x=x^{2}-1$ ( lihat ketentuan di atas )

$\tan \alpha =\frac{x^{2}-1}{-2x}=-\frac{(x^{2}-1)}{2x}$

Uraian 2: $(\sec \alpha - \tan \alpha )^{2} = x^{2}$
$\sec ^{2}\alpha -2.\sec \alpha .\tan \alpha +\tan ^{2}\alpha =x^{2}$
   $\sec ^{2}\alpha -2.\sec \alpha .\tan \alpha +\sec ^{2}\alpha -1=x^{2}$
   $2.\sec ^{2}\alpha -2.\sec \alpha .\tan \alpha -1=x^{2}$
   $2.\sec \alpha (\sec \alpha -\tan \alpha )-1=x^{2}$
   $2.\sec \alpha .x=x^{2}+1$
   $\sec \alpha =\frac{(x^{2}+1)}{2x}$

$Jadi\, (\tan \alpha +\sec \alpha )=-\frac{(x^{2}-1)}{2x}+\frac{(x^{2}+1)}{2x}$
$=\frac{-x^{2}+1+x^{2}+1}{2x}$
$=\frac{2}{2x}=\frac{1}{x}$

Bentuk Baku (Notasi Ilmiah)

00.37 SMP Kelas IX No comments

Bentuk Baku (Notasi Ilmiah)

Bentuk Baku Bilangan Besar

Telah dipelajari bahwa: 100 = 10²

1000 = 10³

1000000 = 10⁶

1000000000 = 10⁹

Bilangan berpangkat positif dengan bilangan pokok 10 di atas dipergunakan untuk menyatakan bentuk baku bilangan besar.

Bentuk baku bilangan besar dinyatakan dengan

$1 \leq a < 10$ dimana $1\leq a< 10^{n}$ n bilangan asli

Contoh:
Nyatakan bilangan-bilangan berikut dalam bentuk baku!
a. 876000 b. 294,5

Penyelesaian:
a. 876000 = 8,76000 x 100000

= 8,76 x 10⁵

b. 294,5 = 2,945 x 100
= 2,945 x 10²

Bentuk Baku Bilangan Kecil
Perhatikan pasangan barisan bilangan berikut
$...,10000,1000,100,10,1,\frac{1}{10},\frac{1}{100},\frac{1}{1000},...$
$...,10^{4},10^{3},10^{2},10^{1},10^{0},10^{-1},10^{-2},10^{3},...$

Dari kedua barisan di atas diperoleh hubungan berikut

$1=10^{0}$
$\frac{1}{10}=\frac{1}{10^{1}}=10^{-1}$
$\frac{1}{100}=\frac{1}{10^{2}}=10^{-2}$
$\frac{1}{1000}=\frac{1}{10^{3}}=10^{-3}$

Bilangan berpangkat negatif dengan bilangan pokok 10 di atas dipergunakan untuk menyatakan bentuk baku bilangan kecil.

Bentuk baku bilangan kecil dinyatakan dengan

$1\times 10^{-n}\, dimana\, 1\leq a< 10\, dan\, n\, bilangan\, asli$

Fungsi

00.11 SMP Kelas VIII No comments

FUNGSI

A. Pengertian Relasi (hubungan)

Bila anggota himpunan A dipasangkan dengan angota himpunan B dengan suatu syarat / aturan tertentu, maka terjadilah relasi dari A ke B

Relasi (hubungan) bisa berupa “kurang dari”, “faktor dari”, “akar dari”, “dua kurangnya dari” dll.

Relasi dapat dinyatakan dengan:

1. Diagram panah

2. Diagram cartesius

3. Himpunan pasangan berurutan

Himpunan

00.05 SMP Kelas VII No comments

HIMPUNAN

A. Pengertian Himpunan

Himpunan adalah kumpulan benda-benda atau obyek yang didefinisikan dengan jelas.

Contoh himpunan

Kumpulan siswa kls 7A yang berkaca mata

Kumpulan binatang berkaki empat

Himpunan lima bilangan prima yang pertama

Contoh bukan himpunan

Kumpulan lukisan yang indah

Himpunan siswa-siswi SMP yang pandai

Pembahasan soal PK dengan cara menfaktorkan

09.22 Soal-soal SMP No comments

Soal:
Tentukan himpunan penyelesaian dari persamaan
x² + (a + b)x + ab = 0

Jawab:
x² + (a + b)x + ab = 0
(x + a) (x + b) = 0
x + a = 0 atau x + b = 0
x = -a x = -b

Jadi Hp nya = { -a , -b }

Ruang Belajar Matematika

About

Ruang Belajar Matematika 1

Ruang Belajar Matematika 2

Ruang Belajar Matematika 3

Ruang Belajar Matematika 4

Ruang Belajar Matematika 5

Rabu, 25 September 2019

Cara Mengetik Rumus atau Simbol Matematika di Blog

Pembahasan Soal Deret Aritmetika

Senin, 23 September 2019

Menyelesaikan Persamaan Kuadrat dengan Menfaktorkan

Selasa, 17 September 2019

Titik Nol

Kamis, 12 September 2019

Pembahasan Soal Trigonometri

Bentuk Baku (Notasi Ilmiah)

Fungsi

Himpunan

Selasa, 10 September 2019

Pembahasan soal PK dengan cara menfaktorkan

Arsip Blog

Categories

BERANDA

Mengenai Saya

Pages - Menu

Pages - Menu

Labels

Blog Archive

Blogger templates

Blogger news

Blogroll

About

Pages

About

Rabu, 25 September 2019

Senin, 23 September 2019

Selasa, 17 September 2019

Kamis, 12 September 2019

Selasa, 10 September 2019

Social Profiles

Arsip Blog

Categories

BERANDA

Mengenai Saya

Pages - Menu

Pages - Menu

Labels

Blog Archive

Blogger templates

Blogger news

Blogroll

About

Pages