Mendapat pertanyaan dari siswa tentang cara menentukan nilai akar tak hingga suatu bilangan, yang mana permasalahan tersebut kecil kemungkinannya dibahas dalam proses pembelajaran. Oleh karena itu pada kesempatan ini Admin mencoba untuk membahasnya.
Salah satu bentuk soalnya sebagai berikut.
Nilai dari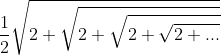 adalah ....
adalah ....
Penyelesaian
 ⇒ disebut bentuk akar tak hingga
⇒ disebut bentuk akar tak hingga
maka
 ⇒ kedua ruas dikuadratkan
⇒ kedua ruas dikuadratkan

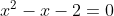 ⇒ penfaktoran bentuk ax2 + bx + c = 0 , dimana a = 1
⇒ penfaktoran bentuk ax2 + bx + c = 0 , dimana a = 1

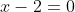 atau
atau 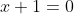
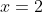
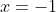 (diambil nilai x yang positif)
(diambil nilai x yang positif)
x = 2, maka nilai
Jadi nilai dari
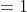
Salah satu bentuk soalnya sebagai berikut.
Nilai dari
Penyelesaian
maka
x = 2, maka nilai
Jadi nilai dari












